下面是是2011年11月24日的SAT官方每日一题的内容，是关于数学方面的，题型是选择。SAT官方每日一题是collegeboard每天都会发布的题目，关于SAT考试的三个部分的各个题型。下面我们就一起来看一下这个SAT官方每日一题吧。

　　SAT官方每日一题之数学---选择：

       有问题?找免费的无忧专家咨询!

　　Mathematics > Standard Multiple Choice

　　Read the following SAT test question and then click on a button to select your answer.

　　The least number of marbles one would need in order to place marbles on each line of the figure above is

　　Answer Choices

　　(A)

　　(B)

　　(C)

　　(D)

　　(E)

　　The correct answer is B

　　Explanation

　　Since a point that is located where two lines intersect is considered to lie on both of those lines, you want to put marbles on as many intersection points of the lines in the figure as possible in order to minimize the number of marbles needed. There are points where two lines intersect. With a marble at each of these locations, there are then exactly marbles on each line of the figure. Thus, the least number of marbles needed is .

　　下面是一道和SAT官方每日一题相似的题目，供大家练习：

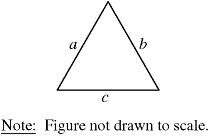
　　If two sides of the triangle above have lengths and , the perimeter of the triangle could be which of the following?

　　.

　　.

　　.

　　Answer Choices

　　(A) only

　　(B) only

　　(C) only

　　(D) and only

　　(E) , , and

　　The correct answer is B

　　Explanation

　　Difficulty: Hard

　　In questions of this type, statements , , and should each be considered independently of the others. You must determine which of those statements could be true.

　　Statement cannot be true. The perimeter of the triangle cannot be , since the sum of the two given sides is without even considering the third side of the triangle.

　　Continuing to work the problem, you see that in , if the perimeter were , then the third side of the triangle would be , or . A triangle can have side lengths of , , and . So the perimeter of the triangle could be .

　　Finally, consider whether it is possible for the triangle to have a perimeter of . In this case, the third side of the triangle would be . The third side of this triangle cannot be , since the sum of the other two sides is not greater than. By the Triangle Inequality, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. So the correct answer is only.

　　以上就是关于2011年11月24日SAT官方每日一题中数学选择的详细内容，包括了题目和选项以及答案，后面附有一道相关的练习题。大家可以在备考SAT的过程中关注SAT每日一题的内容，这样就可以更好有不间断的练习，也就能在日积月累的过程中得到提高。

更多SAT官方每日一题：

2011年11月22日SAT官方每日一题---完成句子

2011年11月23日SAT官方每日一题---改进句子