转载请注明来自无忧留学
Question 1: What is the closest approximation of the solution of the equation 2x - 1 = 3x + 1?(a) -4.42
(b) -5.81
(c) -3.22
(d) 4.93
(e) 3.33
log(2x - 1) = log(3x + 1)(x - 1)log2 = (x + 1)log3
x(log2 - log3) = log3 + log2
x = (log3 + log2)/(log2 - log3)
x is aprox. = -4.418
Question #2: What is the range of (x - y) if 3 < x < 4 and -2 < y< -1?
(a) 4< x-y <5
(b) 1< x-y <3
(c) 1< x-y <5
(d) 4< x-y <6
(e) 3< x-y <6
Answer: We can determine the range of -y:1 < -y < 2
We determine the range of x-y by adding the ranges of x and -y:
Therefore, 4< x-y <6
Question #3: A bus travels the distance d from New York to Boston. t1 hours after the bus left New York, a car starts to travel the same distance d from New York to Boston. Both vehicles reach Boston at the same time. Find an expression for d as a function of t1, the speed of the bus v1 and the speed of the car v2.
(a) d = v1t1/(v2 - v1)
(b) d = v1v2t1/(v2 - v1)
(c) d = v1t1/(v2 + v1)
(d) d = v1v2t1/(v2 + v1)
(e) d = v1v2t1
Answer: If t is the duration of the travel of the bus,d = v1t
d = v2(t - t1)
Therefore, v1t = v2(t - t1)
t = v2t1 / (v2 - v1)
d = v1v2t1 / (v2 - v1)
Question #4:
Find the value of x if:
x + y + z = 5
x + y - z = 3
x - y = 2
(a) -3
(b) -1
(c) 1
(d) 3
(e) 5
Answer: We notice that if we add equations 1 and 2 we can eliminate z: x + y + z + x + y - z = 5 + 32·(x + y) = 8
x + y = 4
At this point we have a system of 2 linear equations with 2 variables, x and y:
x - y = 2
x + y = 4
If we add these 2 equations, we get 2·x = 6 and x = 3.
Question #5: A camera has a price of 300 dollars. Its price is lowered 10% and then increased 10%. What is the final selling price of the camera?
(a) $297
(b) $303
(c) $310
(d) $330
(e) $303
Answer:After it is lowered by 10%, the price is $300 - $30 = $270.
A 10% increase of a $270 price is $27, so the final price is $270 + $27 = $297.
Question #6: The equation 2x2 - 2x - 60 = 0 has the following 2 solutions:
(a) {-5, 5}
(b) {5, -6}
(c) {-5, -6}
(d) {-5, 6}
(e) {5, 6}
Answer: 2x2 - 2x - 60 = 0x2 - x - 30 = 0
The sum of the solutions is 1 and the product is -30 so the solutions are {-5, 6}
Question #7: The side of a cube is two times the radius of a sphere. What is the ratio of the volume of the cube to the volume of the sphere?
(a) 6/¶
(b) 3/¶
(c) ¶/6
(d) ¶/4
(e) ¶
Answer: If l is the side of the cube, the volume of the cube is: Vcube = l3.The volume of the sphere is Vsphere = 4¶r3/3 = 4¶(l/2)3/3 = (¶/6)l3
Vcube/Vsphere = 6/¶
Question #8: If tan(2x) = 2, tan(x) is equivalent to which of the following expressions?
(a) sin(2x)/cos(2x)
(b) 1 + tan(x)
(c) 1 - tan(x)
(d) (1 - tan(x))(1 + tan(x))
(e) (1 - tan(x))2
Answer: tan(2x) = 2tan(x)/(1 - tan2(x))2 = 2tan(x)/(1 - tan2(x))
tan(x) = 1 - tan2(x)
tan(x) = (1 - tan(x))(1 + tan(x))
Question #9: What is the closest approximation of the value of angle a in the figure below, if AB = 7, BC = 11 and CA = 5?
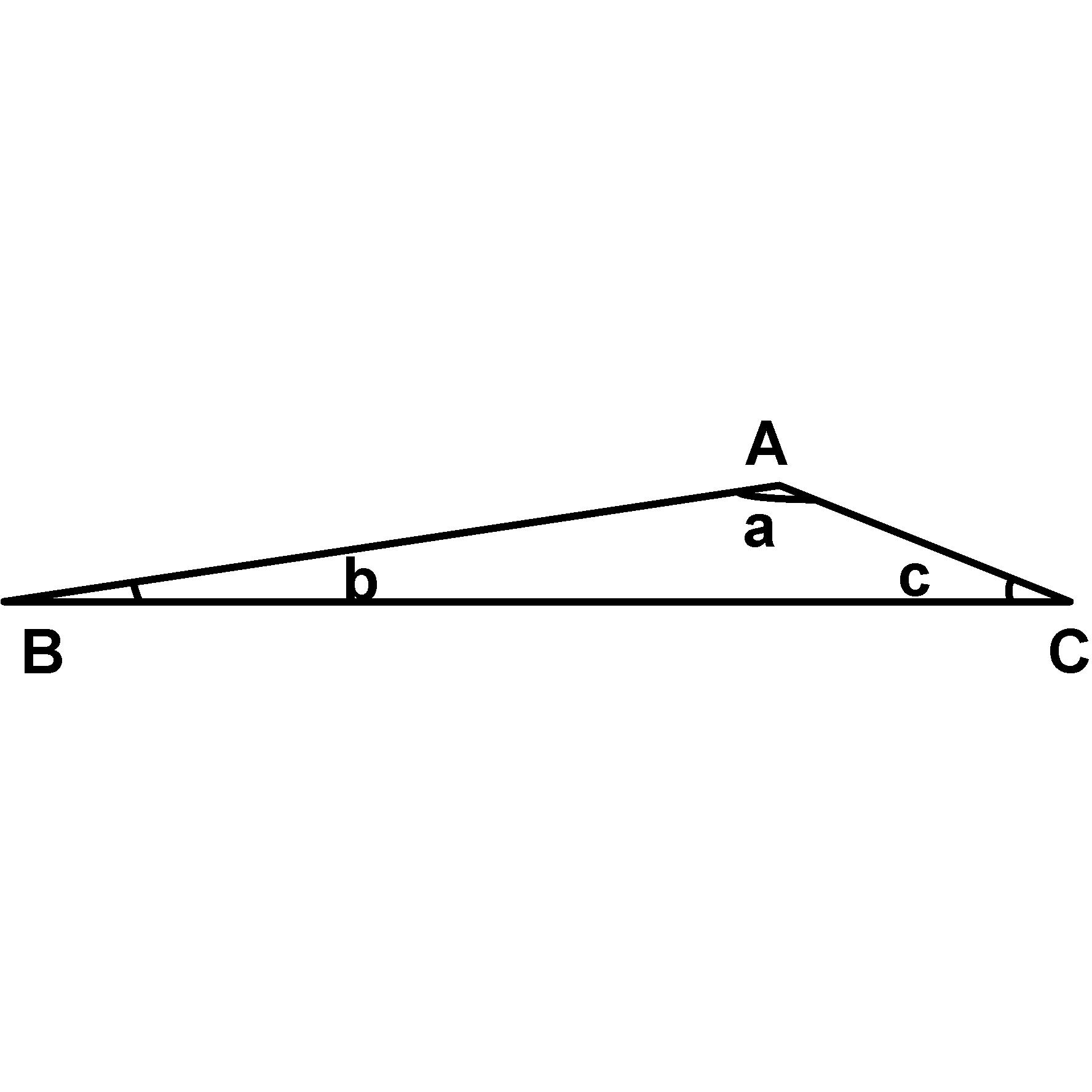
(a) 96.4o
(b) 100.8o
(c) 144.9o
(d) 132.2o
(e) 135.9o
Answer:BC2 = AB2 + CA2 - 2·AB·CA·cos(a)
112 = 52 + 72 - 2·5·7·cos(a)
121 = 25 + 49 - 70cos(a)
cos(a) = -47/70
a = arccos(-47/70) = 132.2o
Question #10: For some positive real number ‘a’, the first 3 terms of a geometric progression are a - 1, a + 3 and 3a + 1. What is the numerical value of the fourth term?
(a) 25
(b) 36
(c) 32
(d) 100
(e) 9
Answer:a + 3 = k(a - 1)
3a + 1 = k(a + 3)
(a + 3)(a + 3) = (3a + 1)(a - 1)
a2 + 6a + 9 = 3a2 - 2a - 1
2a2 - 8a -10 = 0
a2 - 4a -5 = 0
the solutions of this equation are 5 and -1. The only positive solution is 5, so the progression is 4, 8, 16. The fourth term will be 16·2 = 32


