下面是一道SAT2数学题及其解法的相关信息，这是一道关于函数方面的SAT2数学题，属于Level2方面的，难度并不大，但是对大家的逻辑思维水平还是有一些要求的。下面是详细内容，供大家参考，可以先做一下题目，然后在看看解释。
If 
, what value does 
approach as 
gets infinitely larger?
Answer Choices
(A) 
(B) 
(C) 
(D) 
(E) 
The correct answer is E.
Explanation
Difficulty: Easy
One way to determine the value that 
approaches as 
gets infinitely larger is to rewrite the definition of the function to use only negative powers of 
and then reason about the behavior of negative powers of 
as 
gets infinitely larger. Since the question is only concerned with what happens to 
as 
gets infinitely larger, one can assume that 
is positive. For 
, the expression 
is equivalent to the expression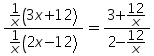 
. As 
gets infinitely larger, the expression 
approaches the value 
, so as 
gets infinitely larger, the expression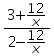 
approaches the value 
. Thus, as 
gets infinitely larger, 
approaches 
.
Alternatively, one can use a graphing calculator to estimate the height of the horizontal asymptote for the function 
. Graph the function 
on an interval with “large” 
, say, from 
to 
.
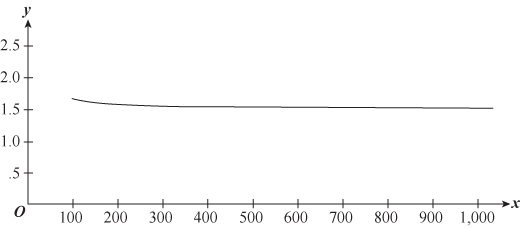
By examining the graph, the 
all seem very close to 
. Graph the function again, from, say, 
to 
.
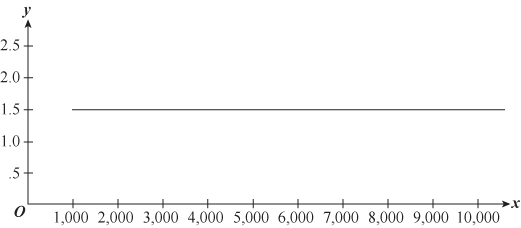
The 
vary even less from 
. In fact, to the scale of the coordinate plane shown, the graph of the function
is nearly indistinguishable from the asymptotic line 
. This suggests that as 
gets infinitely larger, 
approaches 
, that is, 
.
Note: The algebraic method is preferable, as it provides a proof that guarantees that the value 
approaches is 
. Although the graphical method worked in this case, it does not provide a complete justification; for example, the graphical method does not ensure that the graph resembles a horizontal line for “very large” 
such as 
.
以上就是这道SAT2数学题，后面包括了解法，非常详细，以文字和图片两种形式来解析的。SAT2数学考试分成了两个Level，大家可以根据自己的需要选择合适自己的考试项目进行适当的备考。
更多SAT2数学相关信息：
SAT2数学考试内容
Barron SAT2数学习题解答
一道关于渐近线的SAT2数学题
