下面为大家整理的是8道SAT数学练习题的内容，后面都附有详细的答案解析。SAT数学考试是非常注重对考生实际运用知识点能力的考察的，所以大家在备考的时候，一定要多加练习才行。下面我们来看看详细内容吧。
直接获取无忧名师服务点击进入 >>>>有问题?找免费的无忧专家咨询! 或联系QQ客服： ，也可以通过在线咨询处留言，把您最关心的问题告诉我们。
1.A machine can insert letters in envelopes at the rate of 
per minute. Another machine can stamp the envelopes at the rate of 
per second. How many such stamping machines are needed to keep up with 
inserting machines of this kind?
Answer Choices
(A) 
(B) 
(C) 
(D) 
(E) 
1.The correct answer is A
Explanation
First you can change 
minute to 
seconds so that the ratios are both in envelopes per second. One inserting machine inserts letters at the rate of 
per 
seconds, or 
per second. So 
machines would insert 
letters per second.
Let 
be the number of stamping machines needed to keep up with 
inserting machines. Then, since one machine stamps 
envelopes per second, 
machines stamp 
envelopes per second. You can write the equation 
, which gives 
.
2.If 22 times 3 times Q = 6, then Q =
(A) 1 over 11
(B) 1 over 10
(C) 10
(D) 11
(E) 20
2.The correct answer is A
Explanation
The question states that 22 times 3 times Q = 6. Solving for Q gives Q = 6 over (22 times 3) = 1 over 11 when the fraction is reduced.
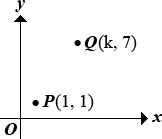
3.In the figure, the slope of the line through points 
. What is the value of 
?
Answer Choices
(A) 
(B) 
(C) 
(D) 
(E) 
3.The correct answer is B
Explanation
The slope of a line in a coordinate plane is given by the fraction whose numerator is the change in 
between any two points on the line and whose denominator is the change in 
between the same points on the line.
The question asks for the value of 
, which is the 
-coordinate of point 
.
The change in 
between points 
and 
is 
. The change in 
between these points is 
. Since the slope is 
, it follows that 
. Solving this equation gives 
. Therefore, 
, and 
.
4.In the 
, line 
is perpendicular to the graph of the function 
. Line 
could be the graph of which of the following functions?
Answer Choices
(A) 
(B) 
(C) 
(D) 
(E) 
4.The correct answer is B
Explanation
If two lines are perpendicular, the product of their slopes is equal to 
. The function 
is in slope-intercept form, so the slope of the graph of 
is equal to 
. Therefore, the slope of line 
must be equal to 
. The only choice that corresponds to a slope of 
is 
.
5.If 
, then 
Answer Choices
(A) 
(B) 
(C) 
(D) 
(E) 
5.The correct answer is C
Explanation
You are given that 
. Dividing both sides of the equation by 
gives
. Thus, the answer is 
.
6.Ten cars containing a total of 
people passed through a checkpoint. If none of these cars contained more than 
people, what is the greatest possible number of these cars that could have contained exactly 
people?
Answer Choices
(A) One
(B) Two
(C) Three
(D) Four
(E) Five
6.The correct answer is D
Explanation
It could not be true that each of the ten cars contained exactly 
people, as this would give a total of only 
. If nine of the cars contained exactly 
people, the remaining car could have no more than 
people, for a total of only 
. Continuing in the same way, a pattern develops. If eight of the cars contained exactly 
people, the remaining two cars could have no more than 
people each, for a total of only 
. If seven of the cars contained exactly 
people, the total number of people could be only 
. From the pattern, you can see that if four of the cars contained exactly 
people, and the remaining six cars contained the maximum of 
people, the total number would be 
, as given in the question. Therefore, at most four of the ten cars could have contained exactly
people.
7.If 
is an odd integer, which of the following is an even integer?
Answer Choices
(A) 
(B) 
(C) 
(D) 
(E) 
7.The correct answer is E
Explanation
If 
is an odd integer, then 
and 
are odd integers. Similarly, choices 
and 
are odd integers. Since an odd integer subtracted from another odd integer is always an even integer, 
is even.
8.If
is the set of positive integers that are multiples of
, and if
is the set of positive integers that are multiples of
, how many integers are in the intersection of
and
?
Answer Choices
(A) None
(B) One
(C) Seven
(D) Thirteen
(E) More than thirteen
8.The correct answer is E
Explanation
The intersection of sets 
and 
is the set of integers that are in 
and also in 
. Set 
consists of all positive integers that are multiples of 
, and set 
consists of all positive integers that are multiples of 
, so the intersection of 
and 
is the set of positive integers that are multiples of both 
and 
. This is the set of all positive integers that are multiples of 
. There are an infinite number of positive integers that are multiples of 
, so there are more than thirteen integers in the intersection of 
and 
.
以上就是这8道SAT数学练习题及答案的详细内容，包括了一些常见的知识点。大家可以在备考的时候，对此加以适当的练习和应用，测试自己在数学方面知识点的掌握情况。
无忧倾情回馈客户，零利润SAT香港考团，详细信息
更多SAT数学相关：
北京SAT数学培训
SAT数学三角函数公式小结
SAT数学备考方法和建议
SAT数学高分备考需摆正心态
