无忧雅思网_雅思预测_雅思机经_雅思考试_雅思资料下载_雅思名师_2018年雅思考试时间

无忧雅思网 > SAT > SAT数学 > 正文

5道SAT数学难题

　　下面为大家搜集了5道SAT数学难题，供大家在备考的时候进行适当的准备。解答SAT数学难题可以比常规的题目更加容易了解SAT数学考试的出题思路和方法。下面我们来看看详细内容吧。

math image

 　　1.Which of the following statements must be true of the lengths of the segments on linemabove?

　　Roman number 1.A B + C D = A D 

　　Roman numeral 2.A B + B C = A D minus C D 

　　Roman numeral 3.A C minus A B = A D minus C D 

　　(A)Roman numeral 1only

　　(B)Roman numeral 2only 

　　(C)Roman numeral 3only 

　　(D)Roman numeral 1andRoman numeral 2only 

　　(E)Roman numeral 1,Roman numeral 2, andRoman numeral 3 

　　2.Ifx + (2 times x)is5more thany + (2 times y), thenx minus y = 

　　(A)negative 5 

　　(B)negative (5 over 3) 

　　(C)3 over 5 

　　(D)5 over 3 

　　(E)5 

math image

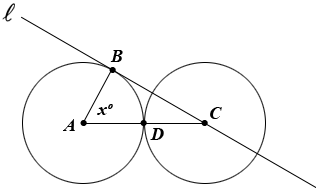
　　3.In the figure above, the circle with center Aand the circle with center Care tangent at point D. If the circles each have radius 10, and if line lis tangent to the circle with center Aat point B, what is the value of x?

　　Answer Choices

　　(A) 55

　　(B) 60

　　(C) 63

　　(D) 65

　　(E) It cannot be determined from the information given.

　　4.A manager estimates that if the company chargespdollars for their new product, where0 less than or equal to p less than or equal to 200, then the revenue from the product will befunction r of p = 2000 times p minus (10 times p^2)dollars each week. According to this model, for which of the following values ofpwould the company’s weekly revenue for the product be the greatest?

　　(A)10 

　　(B)20 

　　(C)50 

　　(D)100 

　　(E)200 

　　5.The length of rectangle Sis twentypercent longer than the length of rectangle R, and the width of rectangle Sis twentypercent shorter than the width of rectangle R. The area of rectangle Sis

　　Answer Choices

　　(A) 20%greater than the area of rectangle R

　　(B) 4%greater than the area of rectangle R

　　(C) equal to the area of rectangle R

　　(D) 4%less than the area of rectangle R

　　(E) 20%less than the area of rectangle R

　　Explanation

　　1.The correct answer is B

　　Consider each statement separately. For example, consider statementRoman numeral 1,A B + C D equals A D. From the figure, you can see that segmentA Dis made up of the segmentsA B,B C, andC D. This tells you thatA B + C Dcannot equalA D, sinceB Ccannot equal zero. StatementRoman numeral 1is not true.

　　Consider statementRoman numeral 2,A B + B C equals A D minus C D. SinceBis betweenAandC, it follows thatA B + B C equals A C. SinceCis betweenAandD, it follows thatA C + C D equals A D. Therefore,A D minus C D = A C. Since bothA B + B CandA D minus C DequalA C, they are equal to each other. StatementRoman numeral 2is true.

　　Consider statementRoman numeral 3,A C minus A B equals A D minus C D. The left side of the equation,A C minus A B, is equivalent toB C. The right side of the equation,A D minus C D, is equivalent toA C. SinceA Bcannot equal zero,B Cis not equal toA C. StatementRoman numeral 3is not true.

　　StatementRoman numeral 2is the only one that is true.

　　2.The correct answer is D

　　The statement given in words translates into the equationx + (2 times y) = y + (2 times y) + 5. This simplifies to3 times x = (3 times y) + 5. Then(3 times x ) minus (3 times y) = 5, and so3 times (x minus y) = 5.

　　It follows thatx minus y = (5 over 3).

　　3.The correct answer is B

　　The circles each have radius 10, so A B = A D = D C = 10. Since the circles are tangent at point D, segment Line ACcontains Dand A C = 20. Also, line A Band lare perpendicular because a line tangent to a circle forms a right angle with the radius at the point of tangency. Therefore, triangle A B Cis a right triangle with hypotenuse 20and side line A Bof length 10. A right triangle with one side of length one-half that of its hypotenuse is a 30 degree-60 degree-90 degreetriangle. The 30 degreeangle is opposite side line A B, so x = 90 minus 30 = 60.

　　4.The correct answer is D

 

　　The graph offunction r of p = 2000 times p minus (10 times p^2)is a downward-facing parabola that intersects thex-axis at0and at200. Parabolas are symmetric, so the maximum value ofroccurs at100, which is halfway between0and200. (Whenp = 100, the value ofrisfunction r of 100 = (2000 times (100)) minus (10 times (100^2)) = 100000.)

　　5.The correct answer is D

　　Represent the length and width of rectangle Ras xand y. Then the area of Ris x times y. The length of rectangle Sis 20%longer than x, which is x = 0.20 times x, or 1.2 times x. Similarly, the width of Sis y minus 0.20 times y, or 0.8 times y. The area of S

is(1.2 times x) times (0.8 times y), which simplifies to 0.96 times x times y. From this it follows that the area of rectangle Sis 4%less than the area of rectangle R.

　　以上就是这5道SAT数学难题的全部内容，后面附有详细的答案解析。大家可以在备考自己的SAT数学考试的时候，进行适当的参考和借鉴之用。

相关推荐